квадрат

Все мы знаем площадь. Четыре секции одинаковой длины, соприкасающиеся под прямым углом. Что вы можете увидеть интересного в нем? Думаю… ничего. Что ж, давайте посмотрим и прочитаем. Во-первых, давайте подумаем, где мы встречаем квадратные формы. Их много вокруг нас.

1. Едем по дороге с преимущественной полосой

Подросток: ты должно быть уже знаешь, что он говорит дорожный знак с рисунка 1.

Упражнение. В какие виды спорта играют на квадратном поле? Позвольте мне привести вам один пример: боксерский ринг. Ищите других.

Теперь своего рода обязательный набор по математике. квадрат со стороной а имеет длину окружности 4а и площадь а². Вот почему вторая степень числа (и, следовательно, его произведение на себя) называется квадратом. Диагональ квадрата равна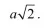 

В моей школе (то есть той, где я учился) важно было помнить, что это примерно 1,4142 — чуть меньше полутора.

Математически говоря, квадрат это прямоугольник. Какой-то особенный, но все же прямоугольник. Это также ромб и дельта. Напомню, что дельтовидная выглядит как воздушный змей (рис. 2). На бытовом языке немного иначе: даже математик скажет: «моя комната не квадратная, а прямоугольная». Однако давайте различать допустимые разговорные выражения и точный язык математики. Например, мне нравится точное определение футбольных репортеров: вратарь укоротил угол. Математически это бессмысленно: угол не имеет длины. Но вы знаете, что происходит.

Да (как в подписи к рис. 2), он отвечает аристотелевским требованиям к определению терминов: По-польски мы переводим это как «ближайшее родовое и видовое отличие». Это можно и нужно понимать так:

• Тип: прямоугольники. Различие видов: равные стороны.
• Тип: алмазы. Видовое отличие: равные диагонали.
• Род: дельтовидные: Видовое отличие: прямоугольные.

Задание (немного математики и немного понимания того, что имел в виду Аристотель). Покажите, что в типе «многоугольники» квадрат отличается видовым различием: 16 площадь = периметр.². Во-первых: упростите то, о чем идет речь.

Вот следующая задача. По опыту мы знаем, что «квадратная» комната устроена хуже, чем прямоугольная (конечно, я употребил здесь оба термина в обыденном смысле) — лишь бы прямоугольник не был слишком «продолговатым». Присутствует ли какая-либо математика?

Конечно есть (как и во всем). Давайте посмотрим на разные комнаты площадью 24 кв.

Мы видим, что чем более вытянут прямоугольник, тем больше его окружность. Мебель в комнате расставлена ​​скорее у стен. Вот почему чем больше окружность, тем больше мы можем установить … пока длина не станет слишком громоздкой. Напомню и принцип золотого сечения. Его можно сформулировать так: целое относится к большей части, а большее к меньшей. Как это выражается математически? Если мы обозначим все через 1, а большую часть через x, мы получим уравнение

после ее решения получаем приближение x = 0,618. Прямоугольник, стороны которого находятся в золотом сечении, выглядит так, как показано на рисунке 4. Добавим, что польский флаг должен быть прямоугольником 8:5, что близко к золотому сечению. Но гостиная такой формы оказалась слишком «продолговатой».

Задача. Докажите, что среди прямоугольников с одинаковым периметром квадрат имеет наибольшую площадь.

Академики склонны доказывать такие факты расчетами. Действительно, если стороны прямоугольника равны х, у, периметр равен 2р, то у = р — х, а площадь ху = х (а — х). Осталось найти наибольшее видимое значение квадратичная функция.

Но они нас интересуют геометрические методы. Посмотрим на рисунок 5. Если прямоугольник не квадрат, то у него неравные стороны. Затем вы можете укоротить одну сторону и удлинить другую, чтобы получить прямоугольник с немного большей площадью. Поле больше поля. Таким образом, только квадрат может иметь наибольшую площадь в классе всех прямоугольников того же периметра. Означает ли это, что квадрат имеет наибольшую площадь в классе всех прямоугольников с таким же периметром? Странный вопрос. Ну, мы только что показали это.

5. Лучше квадрат, чем прямоугольник

Еще нет. Давайте посмотрим на это рассуждение, чтобы «показать», что число 2021 самое большое. Для каждого числа меньше 2021 года можно найти большее число, поэтому 2021 год действительно является самым большим. Где мы делаем ошибку?

Именно здесь мы предполагаем, что вообще существует наибольшее число. Однако предположение неверно, поэтому рассуждения на его основе ничего не стоят и ничего не дают. Нам еще предстоит выяснить, что среди всех прямоугольников одинаковой окружности есть один с наибольшей площадью. Обратите внимание, что такого прямоугольника с наименьшей площадью не существует! И это послужит доказательством того, что самое большое поле достижимо. Если прямоугольник с постоянным периметром очень длинный и узкий, поле близко к нулю. Точно так же, когда он очень высокий с небольшим основанием. Где-то между этими крайностями должен быть максимум.

Я уже напомнил, что диагональ квадрата — иррациональное число 

В настоящее время иррациональность этого числа демонстрируется простыми алгебраическими рассуждениями. Студенты плохо понимают, о чем идет речь. Компьютеры… тоже нет. Иррациональные числа вообще не нужны для практических вычислений. Что я получаю от информации, что для покраски круглого футбольного поля нужен, скажем, килограмм краски. Краска в такой упаковке не продается. В магазине мне все равно приходится конвертировать в «нормальные» числа.

И все же иррациональные числа сыграли чрезвычайно важную роль в истории европейской цивилизации. Пифагору мы обязаны европейской философией познания мира. Его школа-секта первой взглянула на мир глазами разума. Для пифагорейцев все было числами и соотношениями чисел — конечно, только такими числами, как 1, 2, 3, 4,…, 100,… Сегодня мы называем их натуральными числами. И вдруг они обнаружили, что диагональ квадрата это число не… длина диагонали, т.е. Это красивое рассуждение.

В частности, пифагорейцы обнаружили, что диагональ квадрата не соизмерима с его стороной. Не существует такого отрезка, который может уместиться целое число раз и по диагонали, и по бокам. Как доказать, что чего-то нет? Для этого используются косвенные доказательства. Мы используем их неосознанно и каждый день.

Предположим, что сторона квадрата соизмерима с диагональю. На рисунке 6 небольшие участки заполнены как по стороне, так и по диагонали. Длина такого отрезка s называется общей мерой стороны и диагонали. Что мы видим? Это же общая мера меньшего квадрата и его диагонали ВС. Главное, что это одно и то же. Если да, то это будет обычная мера для еще меньшего квадрата и его диагонали. Если да, то это s будет общей мерой для еще меньшего квадрата и его диагонали. Я намеренно повторил предыдущую фразу. Квадраты будут уменьшаться и уменьшаться, а общая мера не изменится. В конце концов, квадраты будут меньше, чем… Этого не может быть. Что-то не так! Какой?

Наше предположение, что эта общая мера вообще существовала, было просто неверным. Она не здесь! Какое рассуждение! Более 2500 лет назад! Может быть, поэтому математика сегодня так трудна, если она уже была такой четверть десятилетия назад (если считать за десятилетие десять тысяч лет)?

Мне очень нравятся задачи по геометрии типа «нарисуй одну линию и ты решишь». Сможете ли вы найти площадь меньшего красного квадрата на рисунке 7? Относительно площади всего квадрата, конечно? Нет? Затем взгляните на рисунок 8 (особенно тот, что справа). Все ясно? Определенно. Приходилось рисовать не одну линию, а на самом деле все это было на бумаге в клетку.

Давайте подойдем к этой задаче иначе. Пусть длина стороны квадрата равна 1. Представьте, что точка неуклонно движется вверх от 0 до 1, увлекая за собой весь квадрат. квадрат он сжимается и поворачивается, когда время t достигает 1, он поворачивается на полные 90 градусов. Но нас интересует не это, а его поле. Давайте посмотрим на рисунок 9. Из теоремы Пифагора посчитаем, что нужно, то есть сторону. Это гипотенуза треугольника. Вот формула площади переменного квадрата. Давайте проверим. Что происходит на полпути между 0 и 1, что является моментом времени

Квадрат изменился на меньший квадрат, как дорожный знак на рис. 1. Квадрат — это половина квадрата.

И вот, когда странник на мгновение останавливается посреди своего пути, есть место для многоэтажного отступления. Вписанный квадрат он устроился как… с Сократом. Ну а в тексте «Менон» (потому что это сложно назвать книгой) Платон описывает, как Сократ учил мальчика геометрии. Он поручил мальчику нарисовать квадрат на песке, а затем нарисуй квадрат в два раза больше. Рисовал мальчик, конечно, как на рис. 10. Грустно констатировать, что 2400 лет спустя Sokratesie Некоторые преподаватели тиражируют эту ошибку, объясняя своим ученикам, что то, что нарисовано в масштабе 1:2, в два раза меньше. Я рекомендую такую ​​аналогию: берем карту Польши в масштабе от одного до миллиона. Это лист размером с развернутую газету. В Польше 38 миллионов жителей, значит, на такой карте поместилось бы 38 человек! Где ошибка рассуждения?

Методом разумно заданных вопросов Сократ заставил мальчика прийти к правильному ответу, разумеется, к тому, который показан на рис. , если использовать современную терминологию, акушерка). Эта теория возрождалась в различных формах и формах на протяжении тысячелетий. Автор этих слов считает, что вся общая дидактика есть лишь вклад в Сократа. Но я не афиширую эту точку зрения.

Отступление должно было быть многоэтажным. Азор, Бурек, Чарусь и Дропс спокойно стоят по углам площади (Рисунок 12). Внезапно Азор почувствовал «что-то» к Буреку, Бурусь к Чареку, Чарек к Дропсу, а Дропс к Азору. Все побежали навстречу друг другу… и что случилось? Собаки делали дуги и, всегда в вершинах поворачивающегося и уменьшающегося квадрата, встречались в самом центре. Физики назвали бы это особой точкой — то, что там произошло, не может быть описано уравнениями. В итоге Анджей, Бася, Целина и Дамиан забрали своих питомцев и даже ни с одним из них не пришлось обращаться к ветеринару. И кривая, по которой они бежали, в математической литературе называется именно так: собачья кривая. Его длина выражается в виде сложного интеграла. Хорошо, что собаки об этом не знают.

Будет еще один уровень отступления. Мы видели, что площадь квадрата, вращающегося как на рисунке 8, равна 2t²-2т + 1. Пусть время течет от нуля до единицы. Вспомним параболу из средней школы, построим график функции y = 2t²-2т + 1. Правильно: в нуле «маленький» квадрат совпадает с большим квадратом, затем сжимается до «сократовского» и с той же скоростью растет. Как частичное солнечное затмение Луной. Такое затмение в астрономии называется кольцеобразным затмением.

Поколения математиков и физиков задавались вопросом, что в уравнениях есть какая-то волшебная мудрость, что в них есть нечто большее, чем мы вкладываем в них. Посмотрим и мы. Что случилось, когда… еще ничего не произошло, когда нас не было на свете? В нашем примере: что было в отрицательное время, например для

Значение функции

Это площадь «малого» квадрата. Как так? Два с половиной? Ведь весь квадрат имеет площадь 1?

Рисунок 14 объясняет это очевидное противоречие. Для отрицательного времени квадрат расположен, как показано на этом рисунке. Рассчитаем его площадь иначе, как обычно. Применим теорему Пифагора к треугольнику. Отрезок имеет длину шесть «квадратов», но за единицу возьмем четыре, поэтому

так что квадрат гипотенузы это как раз то, что

Действительно, уравнение мысли для нас. Просто нужно уметь с ним общаться. С компьютером немного похоже. Он рассчитает, что мы его попросим, ​​но мы должны лично понять, что это барахло выкинуло на экран.

И уже последний этаж отступления. В одной лекции я употребил этот термин: «железо». Присутствовавший в зале видный ученый-компьютерщик, профессор ведущего университета, проинструктировал меня: «Дорогой друг, в компьютере нет ни одного атома железа!». Конечно же, я поблагодарил за эту информацию, и профессор почувствовал благодарность.

В заключение вот викторина; Я подарил его стипендиатам Национального детского фонда на математическом семинаре.

1. Что такое квадратура круга? Это то же самое, что палкой повернуть Вислу вспять, или это имеет другой оттенок смысла?
2. Сколько минут составляет четверть часа? Когда приблизилось шесть часов, ваш прапрадедушка мог бы сказать, что это «три часа из шести». Сколько было времени? Какое это имеет отношение к числу четыре?
3. В каком виде спорта матч делится на четверти? В путеводителе по Татрам 50 века упоминается, что литр сливочного масла стоил 80 центов. А полвека назад, во время поездки на Бабью Гору, я набрал квадратик малины. Так сколько это было? Или, может быть, вы можете играть на пианино кварт? В том же путеводителе сказано, что фотосъемка в стиле кварто стоит XNUMX центов. Насколько большим было это фото?
4. Когда луна находится в первой четверти, она ближе к новолунию или к полнолунию?
5. Когда использовалась квадрига? А может быть вы знаете, что такое геометрическая фигура — квадрика? Скажу лишь, что сфера или поверхность сферы есть. Как вы думаете, что вы получите, если скажете на уроке математики, что, поскольку график линейной функции представляет собой прямую, то квадратичная функция представляет собой квадрат?
6. Если вы станете врачом, вы узнаете о квадрицепсах и квадриплегиках. Я имею в виду что и кого?
7. Генерал приехал инспектировать войска ООН, которые охраняли перемирие в каком-то городе. Казармы были пусты. Полковник пояснил: «В предыдущей четверти нас квартировали в другой четверти» — что это значит?
8. Вы когда-нибудь говорили кому-нибудь: «Ты квадратный осел»? Если так, то это немного грязно, даже если этот кто-то этого заслуживает. 

Смотрите также: