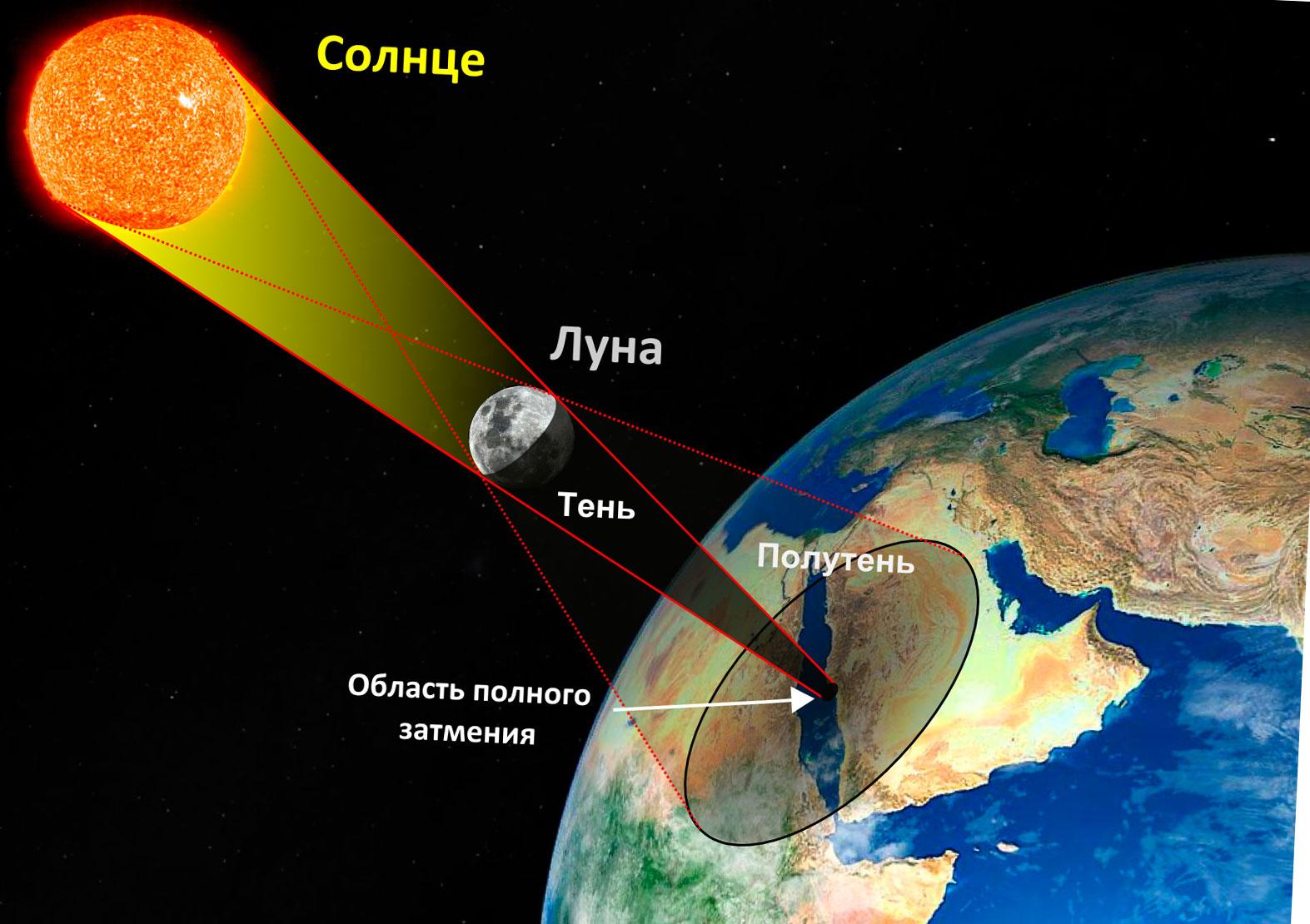
Цветные квадраты и солнечные затмения

В статье описаны мои занятия для учащихся средних классов — стипендиатов Национального детского фонда. Фонд занимается поиском особо одаренных детей и молодежи (от XNUMX-го класса начальной школы до старшей школы) и предлагает избранным ученикам «стипендии». Однако они заключаются вовсе не в снятии наличных, а во всесторонней заботе о развитии таланта, как правило, на протяжении многих лет. В отличие от многих других проектов подобного типа, к подопечным Фонда серьезно относятся известные ученые, деятели культуры, выдающиеся гуманисты и другие мудрые люди, а также некоторые политики.

Деятельность Фонда распространяется на все дисциплины, являющиеся базовыми школьными предметами, кроме спорта, включая искусство. Фонд был создан в 1983 году как противоядие от тогдашней реальности. В фонд может обратиться любой желающий (обычно через школу, желательно до конца учебного года), но, конечно, есть определенное сито, определенная квалификационная процедура.

Как я уже упоминал, статья основана на моих мастер-классах, конкретно в Гдыне, в марте 2016 года, в 24-й неполной средней школе при III средней школе. Военно-морского флота. На протяжении многих лет эти семинары организует под эгидой Фонда Войцех Томальчик, преподаватель необычайной харизмы и высокого интеллектуального уровня. В 2008 году он вошел в десятку лучших в Польше, которым было присвоено звание профессора педагогики (предусмотрено законом многолетней давности). В утверждении: «Образование — ось мира», есть небольшое преувеличение.

и луна всегда завораживают — тогда можно почувствовать, что мы живем на крошечной планете в огромном пространстве, где все находится в движении, измеряемом сантиметрами и секундами. Меня это даже немного пугает, еще и временная перспектива. Узнаем, что следующее полное затмение, видимое из района сегодняшней Варшавы, будет в… 2681 году. Интересно, кто его увидит? Видимые размеры Солнца и Луны на нашем небе почти одинаковы — вот почему затмения такие короткие и такие эффектные. На протяжении веков этих коротких минут должно быть достаточно, чтобы астрономы увидели солнечную корону. Странно, что они случаются два раза в год… но это означает только то, что где-то на Земле их можно увидеть на короткий промежуток времени. В результате приливных движений Луна удаляется от Земли — через 260 миллионов лет это будет так далеко, что мы (мы???) будем видеть только кольцеобразные затмения.

По-видимому, первым предсказал затмение, был Фалес Милетский (28-585 вв. до н.э.). Мы, вероятно, не узнаем, было ли оно на самом деле, то есть предсказал ли он, ведь то, что затмение в Малой Азии произошло 567 мая 566 г. до н.э., является фактом, подтвержденным современными расчетами. Разумеется, я привожу данные по сегодняшнему счету времени. Когда я был ребенком, я представлял, как люди считали годы. Так это, например, XNUMX год до нашей эры, наступает новогодняя ночь и люди радуются: всего XNUMX лет до «н.э.»! Как, должно быть, они были счастливы, когда наконец наступила «наша эра»! Что за рубеж тысячелетий, который мы пережили несколько лет назад!

Математика вычисления дат и диапазонов затмения, не особо сложна, но напичкана всякими факторами, связанными с регулярностью и, что еще хуже, с неравномерностью движения тела по орбитам. Я бы даже хотел знать эту математику. Как мог Фалес Милетский произвести необходимые расчеты? Ответ прост. У вас должна быть карта звездного неба. Как сделать такую ​​карту? Это тоже не сложно, древние египтяне умели это делать. В полночь на крышу храма выходят два священника. Каждый из них садится и рисует то, что видит (как и его коллега). Спустя две тысячи лет мы знаем о движении планет все…

Красивая геометрия, или веселье на «коврике»

Греки не любили числа, они прибегали к геометрии. Это то, что мы будем делать. Наш затмение они будут простыми, красочными, но такими же интересными и реальными. Примем соглашение, что синяя фигура движется так, что затмевает красную. Назовем синюю фигуру луной, а красную — солнцем. Мы зададим себе следующие вопросы:

1. сколько длится затмение;
2. когда половина мишени покрыта;

   Рис. 1 Разноцветный «ковер» с солнцем и луной

3. каков максимальный охват;
4. можно проанализировать зависимость охвата щита от времени? В этой статье (я ограничен объемом текста) я остановлюсь на втором вопросе. За этим стоит приятная геометрия, возможно, без скучных расчетов. Посмотрим на рис. 1. Можно ли предположить, что он будет связан с… солнечным затмением?

Должен честно сказать, что задачи, которые я буду обсуждать, будут специально подобраны, адаптированы к знаниям и умениям учащихся средних и старших классов. Но мы тренируемся на таких заданиях, как музыканты играют гаммы, а спортсмены делают общеразвивающие упражнения. Кроме того, разве это не просто красивый коврик (рис. 1)?

Рис. 2 «Синяя» Луна и «красное» Солнце

Наши небесные тела, по крайней мере на начальном этапе, будут цветными квадратами. Луна синяя, солнце красное (лучше всего для раскрашивания). С настоящим затмение Луна гонится за солнцем по небу, догоняет… и закрывает его. Так же будет и у нас. Самый простой случай, когда Луна движется относительно Солнца, как показано на рис. 2. Затмение начинается, когда край диска Луны касается края диска Солнца (рис. 2), и заканчивается, когда он выходит за его пределы.

Рис. 3 Луна приближается к солнцу по диагонали

Мы предполагаем, что «Луна» перемещается на одну клетку в единицу времени, например, в минуту. Затем затмение длится восемь единиц времени, скажем, минут. Половина солнечные затмения полностью затемняется Половина циферблата закрывается дважды: через 2 и 6 минут. График зависимости «процент затемнения» прост. В течение первых двух минут щит закрывается равномерно со скоростью ноль к 1, следующие две минуты с той же скоростью обнажается.

Вот более интересный пример (рис. 3). Луна приближается к солнцу по диагонали. По нашему соглашению о поминутной оплате затмение длится 8√2 минут — в середине этого времени у нас есть полное затмение. Подсчитаем, какая часть солнца закрыта через время t (рис. 3). Если с начала затмения прошло t минут и в результате Луна такая, как показано на рис. 5, то (внимание!) поэтому покрыта (площадь квадрата APQR), равная половине солнечного диска поэтому накрыли когда, т.е. через 4 минуты (тогда за 4 минуты до окончания затмения).

Рис. 4 График функции «затенения»

Тотальность длится один момент (t = 4√2), а график функции «затененная часть» состоит из двух дуг парабол (рис. 4).

Наша голубая Луна будет касаться угла с красным Солнцем, но оно будет накрывать его, идя не по диагонали, а чуть по диагонали.Интересная геометрия появляется, когда мы немного усложняем движение (рис. 6). Направление движения теперь векторное [4,3], то есть «четыре клетки вправо, три клетки вверх». Положение Солнца таково, что затмение начинается (позиция А), когда стороны «небесных тел» сходятся на четверть их длины. Когда Луна переместится в положение B, она затмит одну шестую часть Солнца, а в положении C затмит половину. В положении D у нас полное затмение, а потом все идет вспять, «как было».

Рис. 5 Часть Солнца, скрытая за время t

Затмение заканчивается, когда Луна находится в положении G. Оно длилось столько, сколько длина участка AG. Если, как и прежде, принять за единицу времени время, за которое Луна проходит «один квадрат», то длина АГ равна. Если бы мы вернулись к прежнему соглашению, согласно которому наши небесные тела 4 на 4, результат был бы другим (что?). Как легко показать, цель закрывается после t < 15. График функции «процент покрытия экрана» можно увидеть на рис. 6.

Рис. 6 График функции «процент защиты»

Уравнение затмения и прыжка

Рис. 7 Обструкция солнечного диска во время затмения, показанного на рис. 6

Проблема затмений была бы неполной, если бы мы не рассмотрели случай кругов. Это гораздо сложнее, но давайте попробуем разобраться, когда одна окружность затмевает половину другой — и в простейшем случае, когда одна из них движется по диаметру, соединяющему их обе. Рисунок знаком держателям какой-нибудь кредитки.

Расчет положения полей сложен, так как требует, во-первых, знания формулы площади кругового отрезка, во-вторых, знания дуги угла, и в-третьих (и самое плохое), умение решать определенное уравнение скачка. Не буду объяснять, что такое «транзитивное уравнение», посмотрим на примере (рис. 8).

Рис. 8 «Сферическое» затмение

Круговое сечение — это «чаша», которая остается после разрезания круга прямой линией. Площадь такого отрезка равна S = 1/2r²(φ-sinφ), где r — радиус окружности, а φ — центральный угол, на который опирается отрезок (рис. 8). Это легко получить, вычитая площадь треугольника из площади кругового сектора.

Эпизод О₁O₂ (расстояние между центрами кругов) тогда равно 2rcosφ/2, а высота (ширина, «линия талии») h = 2rsinφ/2. Итак, если мы хотим рассчитать, когда Луна закроет половину солнечного диска, нам нужно решить уравнение: которое после упрощения принимает вид:

Рис. 9 Графики двух функций

Решение таких уравнений выходит за рамки простой алгебры — в уравнении присутствуют как углы, так и их тригонометрические функции. Уравнение выходит за рамки досягаемости традиционных методов. Вот почему это называется прыгнуть. Давайте сначала посмотрим графики обеих функций, т. е. функций и функций.Приближенное решение мы можем прочитать из этого рисунка. Однако мы можем получить аппроксимацию итеративным методом или… использовать опцию Solver в электронной таблице Excel. Это должен уметь каждый старшеклассник, ведь на дворе 20 век. Я использовал более сложный инструмент Mathematica, и вот наше решение с ненужной точностью в XNUMX знаков после запятой:

SetPrecision[FindRoot[x==Sin[x]+Pi/2,{x,2}],20] {x⇒2.3098814600100574523}.

Рис. 10 Анимация затмения в matematica

Мы превращаем это в градусы, умножая на 180/π. Получаем 132 градуса, 20 минут, 45 и четверть угловой секунды. Рассчитаем, что расстояние до центра окружности равно O₁O₂ = 0,808 радиуса, а «талия» 2,310.